Simulating Chemical Reaction Systems

The following python code simulates deterministic/stochastic mass action kinetics for a reaction system. The repositoriy can be found here

Importing the required libraries for the system

import numpy as np
from scipy.integrate import odeint
from scipy.special import comb,factorial
import matplotlib.pyplot as plt

Helping methods for the MassActionSystem class

y : concentrations
R : set of reactions
k : corresponding rates
t : time (redundant quantity required for odeint)

$\dot{y}(t) = \sum_{l\to r \in R} k_{l\to r}\, y(t)^l \,(r - l)$

def odes(y,t,R,k):
	l = R[:,0] # l, left complex
	r = R[:,1] # r, right complex
	return ((r-l).T).dot(arraypow(y,l.T)*k) 

Method to compute $x^{A}$ :

For matrix $A = (a_{ij})$ and vector $x = (x_i)$ , the notation $x^A$ is the shorthand for the vector of monomials $(\prod _{ i=1 }{x_{i}^{a_{ij}} })$

def arraypow(x,A):
	#Computes(\theta^A)
	return np.prod(x**(A.T),axis=-1)

Reaction System class

Takes in the reactions in form of set of left, right complexes and corresponding rates. Takes in the species symbols, default species are prefixed by “S_”

class ReactionSystem(object):
	"""docstring for ReactionSystem"""
	def __init__(self, reactions, rates, species =None):
		"""Each reaction in reactions is 
		a pair of complex (l,r) in l --> r"""
		reactions = np.array(reactions)
		rates = np.array(rates)*1.0
		self.reactions = reactions
		self.rates = rates
		if species is None:
			species =['S_'+str(i+1) for i in xrange(reactions.shape[2])]
		self.species = species
		

	def display_reactions(self):
		"""
		Puts together the set of reations in a string and returns it
		"""
		reaction_set =""
		for i in xrange(self.reactions.shape[0]):
			l = self.reactions[i][0]
			r = self.reactions[i][1]
			S = self.species
			left_complex =""
			right_complex=""
			for j in xrange(len(S)):
				if (l==0).all():
					left_complex ="0 "

				if (r==0).all():
					right_complex ="0 "
				
				if l[j]:
					left_complex+= " " + str(l[j]) +"("+S[j]+")" + " +"
				
				if r[j]:
					right_complex+=" " + str(r[j]) +"("+S[j]+")" + " +"
			
			reaction = left_complex[:-1] + " ------> " + right_complex[:-1] + "  rate: "+ str(self.rates[i]) + "\n\n"
			reaction_set +=reaction 
		return reaction_set[:-1]

Deterministic Mass Action System class

Inherits ReactionSystem and performs deterministic mass action kinetics on the system

class MassActionSystem(ReactionSystem):
	"""docstring for MassActionSystem"""
	def __init__(self, reactions, rates, species =None):
		# super(MassActionSystem, self).__init__()
		super(MassActionSystem,self).__init__(reactions, rates, species)

	def set_concentrations(self,concentrations):
		"""
		Sets the concentration of the species
		"""
		concentrations = 1.0*np.array(concentrations)
		if concentrations.shape[0] == self.reactions.shape[2]:
			self.concentrations = concentrations
		else:
			print "Wrong Initialization: Shapes of concentrations and reactions dont match ",\
			concentrations.shape[0], "!=", self.reactions.shape[1]
		return self.concentrations

	def dydt(self):
		"""
		Returns rates of concentrations change at the current concentration
		"""
		return odes(self.concentrations,0,self.reactions,self.rates)

	def current_concentrations(self):
		"""
		Returns the concentrations after the latest run
		"""
		return self.concentrations

	def run(self,t=1000,ts=100000,plot=False):
		"""
		Run it for time t with ts number of time steps
		Outputs the concentration profile for the run
		default values are 100000 and 1000000
		"""	
		t_index = np.linspace(0, t, ts)
		y = self.concentrations
		output = odeint(odes, y, t_index, args= (self.reactions,self.rates))
		self.concentrations = output[-1,:]
		if plot:
			for i in xrange(output.shape[1]):
				label = self.species[i]
				plt.plot(t_index, output[:, i], label=label)
			plt.legend(loc='best')
			plt.xlabel('t')
			plt.title('Concentration Profile')
			plt.grid()
			plt.show()
		return output

Stochastic Mass Action System

An implementation of the Gillespie Algorithm on a Reaction System. These slides might help understanding the stochastic simulation.

class StochasticSystem(ReactionSystem):
		"""docstring for StochasticSystem
			Gillespie Algorithm implementation
		"""
		def __init__(self, reactions, rates, species =None):
			"""TODO: Maybe add a method to make sure reaction
			coefficients are integers"""
			super(StochasticSystem, self).__init__(reactions, rates, species)
				
		def set_population(self,population):
			population = 1.0*np.array(population)
			if population.shape[0] == self.reactions.shape[2]:
				self.population = population
			else:
				print "Wrong Initialization: Shapes of population and reactions dont match ",\
				 population.shape[0], "!=", self.reactions.shape[1]
			return self.population

		def current_population(self):
			return self.population

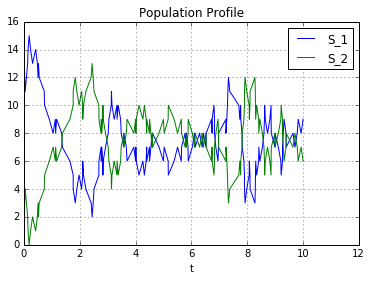
		def run(self, t,seed=None,plot=False):
			"""
			Gillespie Implementation
			"""
			l = self.reactions[:,0]
			r = self.reactions[:,1]
			change=r-l
			time =0
			times =[]
			output =[]
			times.append(time)
			output.append(self.population)
			while time<t:			
				lam = np.prod(comb(self.population,l)*factorial(l),axis=-1)*self.rates
				lam_sum = np.sum(lam)
				dt = np.log(1.0/np.random.uniform(0,1))*(1.0/(lam_sum))
				react = np.where(np.random.multinomial(1,lam/lam_sum)==1)[0][0]
				self.population = self.population + change[react]
				time += dt
				output.append(self.population)
				times.append(time)
			output = np.array(output)
			times = np.array(times)
			if plot:
				for i in xrange(output.shape[1]):
					label = self.species[i]
					plt.plot(times, output[:, i], label=label)
				plt.legend(loc='best')
				plt.xlabel('t')
				plt.title('Population Profile')
				plt.grid()
				plt.show()
			return times,output

Main

Simulating for simple examples:

def main():
	reactions = [[[1,0,1],[0,2,0]], [[0,2,0],[1,0,1]]]
	rates = [1,1]
	system = MassActionSystem(reactions,rates)
	print "Reactions:"    
	print system.display_reactions()    
	system.set_concentrations([-0.1 + 1/3.,0.2 + 1/3.,-0.1 + 1/3.])
	print "Initial Concentrations:",system.current_concentrations()    
	system.run(t=10,ts=1000,plot=True)
	print "Final Concentrations:",system.current_concentrations()
	print "Final concentration change rates:", system.dydt(),"\n\n\n"

	# Simulating Stochastic System
	reactions = [[[1,0],[0,1]], [[0,1],[1,0]]]
	rates = [1,1]
	system = StochasticSystem(reactions,rates)
	print "Reactions:"    
	print system.display_reactions()
	population = [15,0]
	system.set_population(population)
	print "Initial Population:",system.current_population()  
	t,o = system.run(10,plot=True)
	return

if __name__ == '__main__':
	main()

Reactions:
 1(S_1) + 1(S_3)  ------>  2(S_2)   rate: 1.0

 2(S_2)  ------>  1(S_1) + 1(S_3)   rate: 1.0

Initial Concentrations: [ 0.23333333  0.53333333  0.23333333]

png

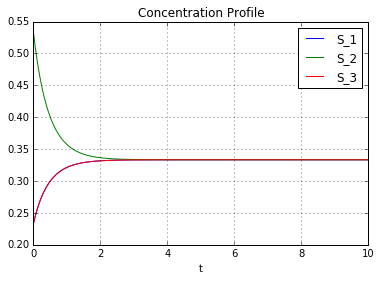
Final Concentrations: [ 0.33333333  0.33333333  0.33333333]
Final concentration change rates: [  1.79787518e-10  -3.59575036e-10   1.79787518e-10] 

Reactions:
 1(S_1)  ------>  1(S_2)   rate: 1.0

 1(S_2)  ------>  1(S_1)   rate: 1.0

Initial Population: [ 15.   0.]

png

What's your go-to joke? »

Viswa Virinchi

Reaction System Simulator!

Simulating Chemical Reaction Systems

Importing the required libraries for the system

Helping methods for the MassActionSystem class

Method to compute $x^{A}$ :

Reaction System class

Deterministic Mass Action System class

Stochastic Mass Action System

Main

Viswa Virinchi

Reaction System Simulator!

Simulating Chemical Reaction Systems

Importing the required libraries for the system

Helping methods for the MassActionSystem class

Method to compute x^{A}:

Reaction System class

Deterministic Mass Action System class

Stochastic Mass Action System

Main

Method to compute $x^{A}$ :